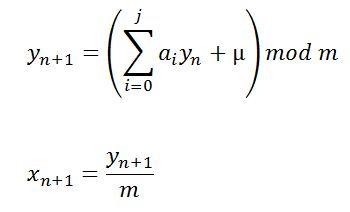Congruential Method of Formation of Pseudo-Random Numbers
We need to program a generator of pseudo-random numbers using the congruential method of formation of pseudo-random numbers.
Random numbers means the possible values xi of a continuous random variable X, distributed uniformly on the interval [0;1).
The formula defining the congruential method of generating pseudo-random numbers is represented like this:
where, a0, a1, . . . aj — multipliers
µ — increment value
y1, y2, . . . yn — resulting random number
x1, x2, . . . , xn — random numbers on the interval [0;1)
The program generates 15 random numbers, and for the result of the program see below. All the random numbers lie in the interval [0;1).
So considering the formula we should obtain such result:
0.81 0.13 0.69 0.17 0.01 0.73 0.49 0.57 0.21 0.33 0.29 0.97 0.41 0.93 0.09 0.37 0.61 0.53 0.89 0.77 0.81 0.13 0.69 0.17 0.01 0.73.
Let’s try to implement it using C++ tools. All necessary comments will be included:
[code language=”cpp”]
#include "stdafx.h"
#include <iostream>
using namespace std;
double pseudo(int &); // prototype for pseudo-random function
int main(int argc, char* argv[])//comand prompt arguments
{
const int amount = 25; // amount of pseudo-random numbers
int x0 = 2; // starting value
cout << "\nPseudo-random: ";
for (int i = 0; i <= amount; i++)
cout << pseudo(x0) << " "; // generate the i-th number
cout << "\n";
system("pause");
return 0;
}
double pseudo(int &x) // generating pseudo-random numbers function
{
const int a = 100, // generating pseudo-random numbers from 0 to 100
m = 8, // multiplier
increment = 65; // increment value
x = ((m * x) + increment) % a; // out formula
return (x / double(m));
}
[/code]
Let’s try to run the program. Here is what we get:
Pseudo-random: 0.81 0.13 0.69 0.17 0.01 0.73 0.49 0.57 0.21 0.33 0.29 0.97 0.41 0.93 0.09 0.37 0.61 0.53 0.89 0.77 0.81 0.13 0.69 0.17 0.01 0.73
Everything works correctly. There are a lot of more complicated ways to implement the solution of this task, but in this guide we concentrated on the most simple one.
Thanks for your attention!
Superior Help With Information Technology Assignments
You can freely use this program for the generation of pseudo-random numbers using C++ tools. Our samples are aimed to help you with conducting your own assignments more easily and effectively. Keep in mind that if you plan to take parts of our essay sample and include them in your own writing, you may be accused of plagiarism. If you were assigned an unmanageable assignment and you need assistance, don’t be upset! Use AssignmentShark.com and professionals will take care of your papers.
If you are studying in an IT related course, you should pay a lot of attention to the practical part of your studying, and most likely you would like to apply the generation of pseudo-random numbers using C++ tools in practice. We clearly understand that students don’t want to waste time on monotonous and sometimes useless essays and reports. In any case, you can rely on our service in order to spend your time more effectively, and at the same time receive good grades. Our team of writers is able to complete any paper on any discipline, so be confident that your assignment will be in the hands of professionals. To make the order, you should fill in the order form and describe the requirements of your assignment, set the deadline, and add contact info. Our experts will put every effort into making your paper unique and of the best quality.
Do my computer science assignment right now!