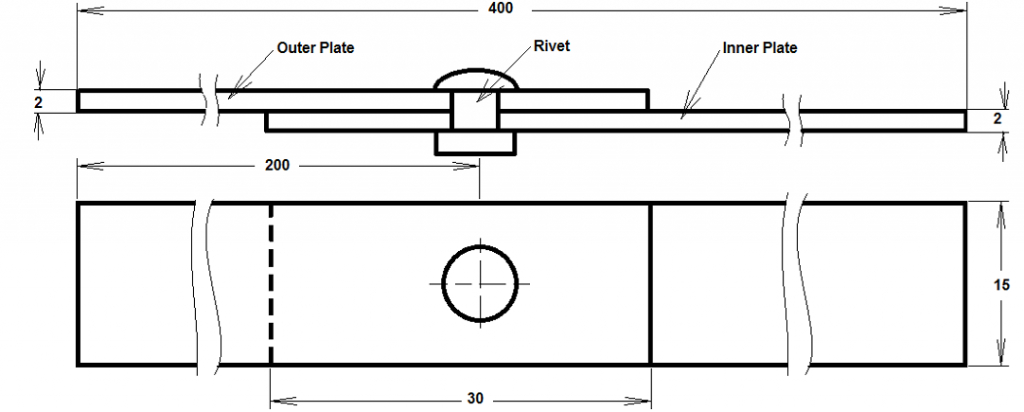
Problem statement: There is a lap joint with one rivet, as shown in the Figure 1 below. The diameter of the rivet is 4 mm. The material of the rivet, as well as the material of pates in joint are given in the table 1 below. Force which is applied to the plate is given in form of distributed force through the cross-sectional area of the plate. Perform the Stress Analysis of the joint in order to verify the durability of the junction.
Figure 1. Lap joint
Table 1. Material properties
| Material | Young’s Modulus | Poisson’s Ratio | |
| Plate | 2024-T3 | 74 GPa | 0.33 |
| Rivet | 2117-T4 | 71.7 GPa | 0.33 |
Solution:
There are four main theories of Failures of Rivet Joints, which are as follows (Dhananjay, n.p.):
- tearing of the plate at an edge;
- tearing of the plate across a row of rivet;
- shearing of rivet;
- crushing of the plate (or) rivet.
The force which was applied in the joint was given in terms of unit force, therefore the total force can be found as multiplication of the unit force on the cross section area of the plate. Since both outer and inner plates have the same dimensions, their cross-section areas are the same too, therefore:
Where P is the unit force; A is the cross-sectional area.
![A=2*15=30[mm^2]](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-08cecdd987ad3f1272195db4b61de2af_l3.png "Rendered by QuickLaTeX.com")
![F=68.6*10^6*30*10^{-6}=2058[N]](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-f7043639b915e4e2a35e223a9a9585d9_l3.png "Rendered by QuickLaTeX.com")
The maximum stress due to crushing is:
![\sigma _{c}=\frac{F}{dt}=\frac{2058}{4*2}=257.25[Mpa]](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-0e4d425e52d6fa1289bd7d135a3ec49c_l3.png "Rendered by QuickLaTeX.com")
Where
is the river diameter;
is the plate thickness.
Tearing of the rivet through a row of rivet 
![\sigma _{t}=\frac{F}{(p-d)*t}=\frac{2058}{(15-4)*2}=93.54[Mpa]](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-e39d768ef53130a8801cf8e9b4e01b73_l3.png "Rendered by QuickLaTeX.com")
Shearing of rivet 
![\tau _{s}= \frac{F}{\pi d^{2} / 4} = \frac{2058}{\pi 4^{2} / 4} = 163.77[Mpa]](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-eb036a9f6f674d601dfee8b962e58e30_l3.png "Rendered by QuickLaTeX.com")
Maximum Shear Stress:
![\tau_{max} = \frac{1}{2} \sqrt{\sigma_{t}^{2} + \tau_{s}^{2}} = \frac{1}{2} \sqrt{(93.54)^{2} + (163.77)^{2}} = 107.31[Mpa]](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-343434bbcf5a2eb6c6a16ac8a9fffe23_l3.png "Rendered by QuickLaTeX.com")
As could be seen from the calculations, the maximum stress which occur in the plate due to the loading is 257.25 Mpa, which is less than the yielding stress of the plate material (74Gpa).
The maximum stress which occur in the rivet due to the loading is shearing stress, which is 163,77 Mpa, which is also much lower than the yielding stress of the rivet material, equaled to 71.7 Gpa.
The Efficiency of Riveted joint can be obtained as follows:
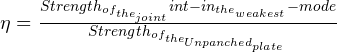
Therefore, the efficiency of the joint is:
Conclusion: The lap join is durable under the given loading, since the maximum stresses which occur in plates and rives are much lower that the maximum allowable stresses.
References:
Dhananjay A Jolhe “Engineering Graphics”, (n.p.). Department of Industrial Engineering. Shri Ramdeobaba Kamla Nehru Engineering College. Nagpur. Extracted from:
http://www.ignou.ac.in/upload/Unit-3-60.pdf
You have come to the right place if you need good engineering samples for inspiration. We remind you that you are not allowed to use this assignment, as well as any others posted at our blog, as your own, since it will be considered as plagiarism. But we understand that sometimes college or university can be hard, and you want to do so not because you are an evil person, but because you are desperately trying to compose something descent out of engineering samples you find on the Internet. Your struggle is over! Place your order and receive help with assignment without doing anything more complicated than clicking your mouse.
You can also check our engineering problem solving sample posted before.