Element Search Algorithm in the Sorted Matrix of Size NxN
To find the desired item we can use a binary search for each line. The algorithm requires O (M log (N)) time as it is necessary to process the M columns, for each of which we spend O (log (N)) time. We will analyze this method.
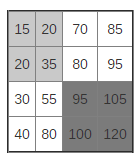
Let’s take a look at the example:
Let’s ask ourselves: where can the elements be?
We know that all the rows and columns are sorted. It means that the element [i] [j] is greater than the elements in row i lying between 0 and j column and j row elements between lines 0 and i-1.
In other words:
[code language=”cpp”]
a[i][0] <= a[i][1] <= … <= a[i][j-i] <= a[i][j]
a[0][j] <= a[1][j] <= … <= a[i-1][j] <= a[i][j]
[/code]
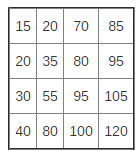
Let’s look at the matrix: The element, which is in dark gray cell, is greater than the other selected elements.
White cell elements are sorted. Each of them is more like a left element and an element located above. Thus, the highlighted item is bigger than the elements in the square.
It is possible to formulate a rule: the lower right corner of any rectangle selected in the matrix will contain the largest element.
Similarly, the upper left corner is always the smallest. The colors in the diagram below reflects information about ordering elements (light gray<white<dark gray):
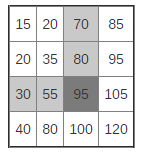
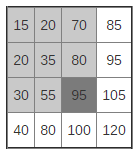
Let’s go back to the original problem. Let us assume that we need to find the element 85. If we look at the diagonal, we see the elements 35 and 95. What kind of information on the location of the element 85 can be learned?
85 can not be in the dark gray area since the element 95 located in the upper left corner is the smallest element in this square. 85 can not belong to the light gray area, as the element 35 is in the lower right corner. 85 should be in one of the two white areas.
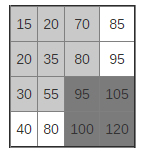
Thus, we divide our grid into four quadrants and search in the lower left and upper right quadrants. They can also be divided into quadrants, and the search can be continued.
Note that the diagonal is sorted, which means that we can effectively use binary search.
Thanks for your attention!
Get Help with the Assignments Here
Are you stuck with your programming assignment? Don’t worry, the solution is near – all you need to understand about how the task should be solved is a good example of binary search, and you’ve come to the right place. We at AssignmentShark are always ready to provide you with quality samples done by our awesome programming professionals. Check our blog for more fresh samples and articles on learning advice.
You can always rely on us if you have been assigned a difficult task. You can either check our blog for new samples which can be helpful in finding your own solution, or place an order and receive your personal example of binary search completed by our experienced programming specialists.
So what do you need to do to get assignment help online? First of all, fill in the short form at the top right corner of the page. You will be automatically taken to a page with a longer form, where you need to answer more specific questions about your assignment, such as formatting, volume, additional files and commentary. Once you are done with this part, you will be asked to choose a professional from the list of those who stated they were interested in your order. Now programming doesn’t sound so terrifying, right?
You can also get assistance with any of the disciplines you face difficulties with – simply ask us “do my accounting assignment,” for example, and rely on our experts.