Theory
Heap Sort is classical algorithm which, perhaps any programmer should know. This sorting algorithm is notable for the fact that regardless of the data set it has one and the same complexity time – O (n log n).
Heap sort uses binary sorting tree. The sorting tree is a tree based on such conditions: aach sheet has a depth “d”, or “d-1”, where d is a maximum depth of the tree. The value in each vertex has not less (another option not bigger) value than its descendants.
Convenient data structure for sorting tree is an array Array, where Array[1] is the element at the root, and the descendants of the Array elements [i] are Array [2i + 1] and Array [2i + 2].
The sorting algorithm will consist of two main steps:
- The elements of the array are building a sorting tree:
Array[i] ≥ Array[2i+1]
Array[i] ≥ Array[2i+2] - Remove items from the root by one at a time and rebuild the tree. On the first step exchange the Array[1] and Array [n], convert Array[1], Array[2], …, Array[n-1] in the sorting tree. Then swap Array[1] and Array[n-1], convert Array[1], Array[2], …, Array[n-2] in the sorting tree. The process continues until the tree contains one element. Then Array[1], Array[2], …,Array [n] constitute an ordered sequence.
This step requires O (n \ log n) operations.
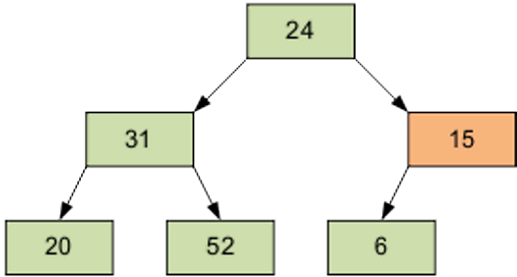
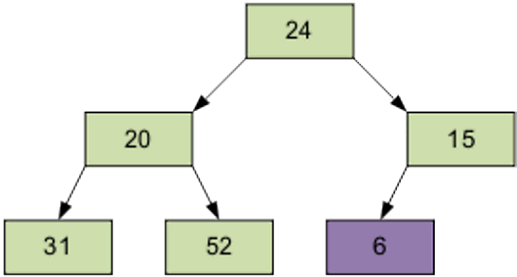
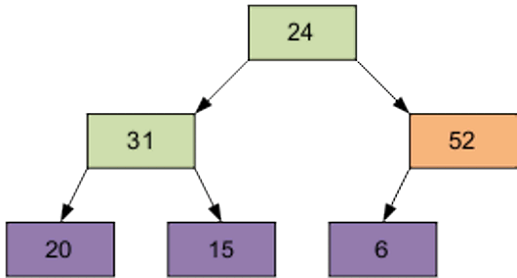
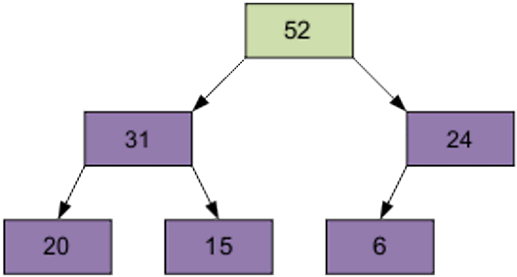
For example let’s sort such array: 24, 31, 15, 20, 52, 6
Stage 1
Arrange the items in the original form of the tree; the number of the element in the right part is (6 / 2-1) = 2 – this element is – 15.
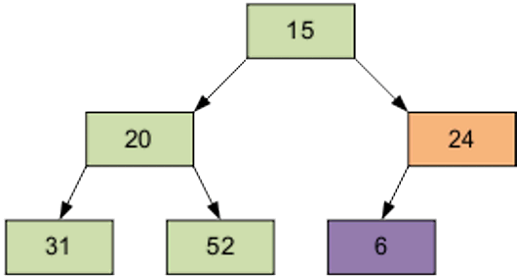
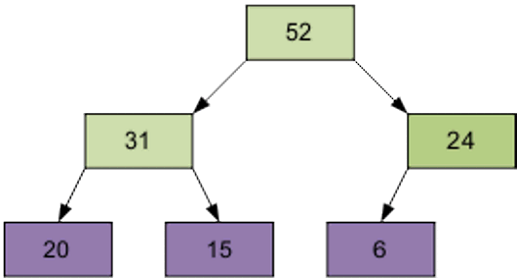
The result of the screening element 15 through the pyramid.
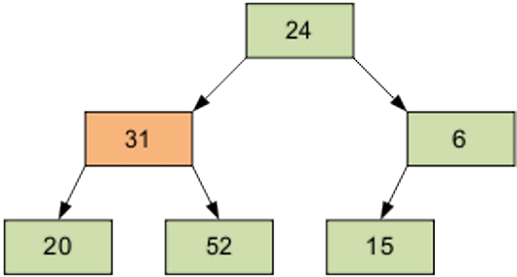
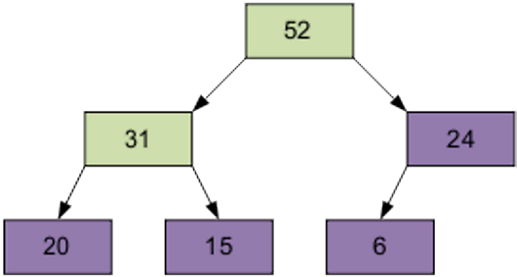
Next screening element is 1, equal to 31.
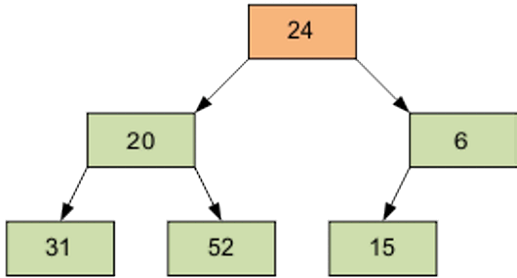
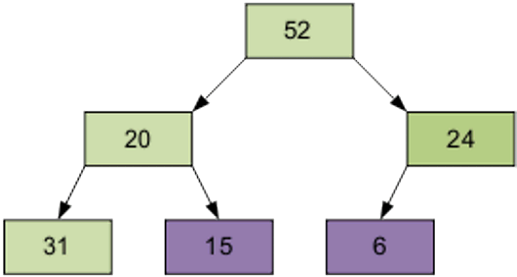
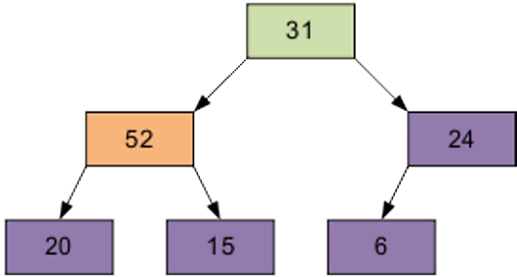
Then – item 0 equal to 24.
Of course, the resulting array is not sorted. However, the procedure of screening is the basis for the heapsort. As a result of screening the smallest element is on top of the pyramid.
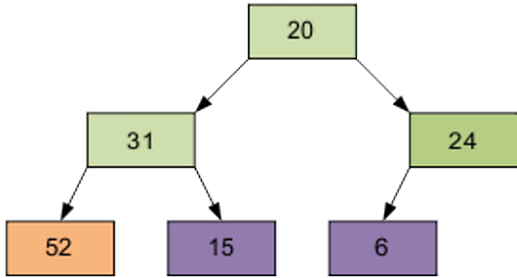
Stage 2
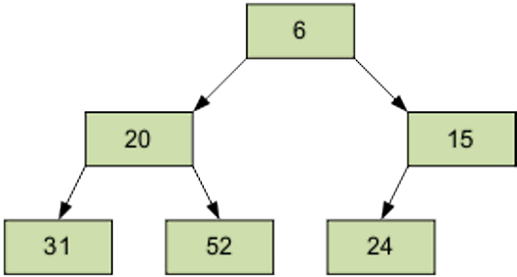
Sorting the tree. We take the last element of the array as the current. Swap the top (smallest) element of the array and the current. Sift through current member (now it’s the top) through n-1 elemental pyramid. Then take the penultimate element, etc.
Continue the process. As a result, the array will be sorted in descending order.
So that’s how the array is sorted. Here’s the screenshot of execution of the program with such array: {56,3,3,5,78,34,21,43,54,23,4,5,7,8,6,4,23,23,4}
And here is the Java code:
[code language=”cpp”]
public class HeapSort {
private static int[] arr;
private static int size;
private static void output(int[] arr) {
int count = 0;
while (count < arr.length) { System.out.print(arr[count++] + " "); } System.out.println(""); } private static int ancestor(int count) { return ((count + 1) / 2 – 1); } private static void swap(int a, int b) { int tmp = arr[a]; arr[a] = arr[b]; arr[b] = tmp; } private static int leftHeap(int count) { return ((count + 1) * 2 – 1); } private static int rightHeap(int count) { return ((count + 1) * 2); } private static void maxHeap() { int count = arr.length / 2 – 1; size = arr.length; while (count >= 0) {
doMaxHeap(count);
count–;
}
}
private static void doMaxHeap(int count) {
int largest = count;
int left = leftHeap(count);
int right = rightHeap(count);
if (right < size) {
if (arr[largest] < arr[right]) {
largest = right;
}
}
if (left < size) {
if (arr[largest] < arr[left]) { largest = left; } } if (largest != count) { swap(count, largest); doMaxHeap(largest); } } public static void sorting(int[] tmp) { arr = tmp; sorting(0, arr.length); } private static void sorting(int leftHeap, int rightHeap) { int count = arr.length – 1; maxHeap(); while (count > 0) {
swap(0, count);
size -= 1;
doMaxHeap(0);
count–;
}
}
public static void main(String[] args) {
int[] arr = {56,3,3,5,78,34,21,43,54,23,4,5,7,8,6,4,23,23,4};
System.out.println("Your array:");
output(arr);
System.out.println("Sorting…");
sorting(arr);
System.out.println("Sorted array:");
output(arr);
}
}
[/code]
This assignment is a Heapsort Java example created by our programming experts to provide you with a good sample of how such papers should be written. You are not allowed to use any parts of this assignment in any way that violates the author’s rights. If you need assignment help with your programming project, we are always ready to provide it! Place your order and receive your very own Heapsort Java example to learn from. We guarantee you top-notch quality, on-time delivery and protection of your personal information. Being a student is hard unless you work with AssignmentShark academic experts.
You can also find useful gravity calculator Java example posted on our blog several months ago.