Quicksort Example

Do you need to take a look at a Quicksort example? You can find a good sample below. It was completed by an expert from AssignmentShark in accordance with our requirements. We offer you the ability to look through this sample and other examples on our website for free. All of them, including the one that is provided below, were prepared by experts that have vast experience in certain disciplines and topics.

If you need a more specific Quicksort example, you can ask us to complete it for you. The only thing you need to do is to describe your requirements accurately and our experts will help you to cope with your task. Why is it convenient? More specific examples will help you to understand better the regularities of completing specific tasks. This option is paid because experts will complete examples especially for you, and no one else will get the same example.

All of the experts that complete samples are accredited with high-level degrees. This means that they are knowledgeable in academic standards and they have a lot of experience in completing diverse academic tasks. For this reason, you can be confident that our samples are high-quality.

Before making an order, you should get acquainted with our free samples. They will probably help you. If they don’t, contact us and we’ll do our best to provide you with more help.

Hello! In this guide, I will tell you about the algorithm called Quicksort and show how to implement it using the C programming language.

So, Quicksort is an efficient sorting algorithm. On average, it performs O(n log n) comparisons to sort the array with n elements. In the worst case, it will perform O(n2) comparisons.

The essence of the algorithm is pretty simple: we choose the bearing element and then divide the array into three parts: less then the bearing element, equal to the bearing element, and bigger than the bearing element. Then, the algorithm is recursively applied to subarrays.

Program algorithm:

1. Choose the bearing element.
2. Divide the array into three parts:
   • Create l and r variables which are assigned to the indexes of the beginning and the end of the considered subarray.
   • Increase l while the element number l is less than the bearing element.
   • Decrease r while the element number r is bigger than the bearing element.
   • If l is still less then the r, swap the element number l and element number r, increment l and decrement r.
   • If l is bigger than r, break the cycle.
3. Repeat first two steps recursively until we reach the array consisting of 1 element.

So, let’s take a look at the implementation of the algorithm in the C programming language:

[code language=”cpp”]
void Quicksort(int a, int b)
{
int l = a, r = b;
int bear = array[(l + r) / 2]; // choose the middle element as the bearing one
while (l <= r)
{
while (array[l] < bear) l++; while (array[r] > bear)
r–;
if (l <= r)
swap(array[l++], array[r–]);
}
if (a < r) qsort(a, r); if (b > l)
qsort(l, b);
}
[/code]

This realization has a lot of disadvantages, such as a possibility of the stack overflow because of a large number of nested recursions and the fact that the bearing element is always the middle one. Usually, it works normally, but in solving, for example, Olympiad problems, a tricky jury can specifically choose such tests so this solution will work too long and won’t pass the limit.

The dependence of the performance of the bearing element is one of the main disadvantages of the algorithm, and nothing can be done about it. If you need the sorting algorithm that will work with a guaranteed O(n log n) speed, you should prefer the Pyramid Sort. But usually, Quicksort is more productive than the others. It doesn’t require too much memory and it’s simple in the implementation, therefore its popularity is deserved.

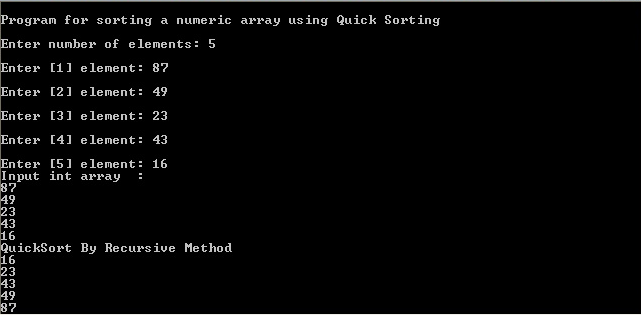
Here is a screenshot of the working program:

Thanks for your attention!