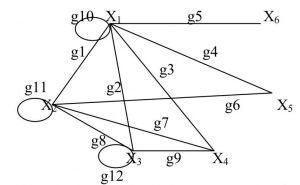
In the example you can read below, you can get information about the relationship graph solution that was written by one expert from AssignmentShark. If you have problems with understanding a particular math assignment, you can ask for help from one of our math gurus! “I look for someone to do my homework for free. ” – Our help won’t be completely free, but you can learn from the examples yourself, or get advice for the future from our experts.
When students are taking math classes, they frequently have problems with understanding all of the material. Also, math tutors usually give a lot of complex homework that not every student can do. Students can find assistance in books, but in a tight studying schedule you need to set priorities between disciplines and personal life. With online assignment help of our service you can receive expert help with homework on various disciplines, so you can spend more time on more things that are important for you.
Don’t give up even if you struggle with your relationship graph assignment and are ready for failure. You can rely on assignment help from online experts. For the AssignmentShark team we have gathered professionals from many fields: physics, math, programming, and many more. Here you can receive unique, high-quality homework assistance that will be delivered strictly on time. Make an order and stay calm: your homework will be done on time.
Task:
Construct a graph of the following relationship:
Define its properties.
Solution:
Construct graph G( X ) with the set of vertices ![]() , and two vertices X i and X j are connected by an edge if and only if
, and two vertices X i and X j are connected by an edge if and only if ![]() . Since the relation
. Since the relation ![]() is symmetric, graph G( X ) is undirected.
is symmetric, graph G( X ) is undirected.
Let’s construct the adjacency matrix (vertices) A:
| X1 | X 2 | X 3 | X 4 | X 5 | X 6 | |
| X1 | 1 | 1 | 1 | 1 | 1 | 1 |
| X 2 | 1 | 1 | 1 | 1 | 1 | 0 |
| X 3 | 1 | 1 | 1 | 1 | 0 | 0 |
| X 4 | 1 | 1 | 1 | 0 | 0 | 0 |
| X 5 | 1 | 0 | 0 | 0 | 0 | 0 |
| X 6 | 1 | 0 | 0 | 0 | 0 | 0 |
Here Aij element is the number of edges going from vertex X i to vertex X j . As our graph is undirected, the adjacency matrix is symmetric.
Let’s construct the incidence matrix (ribs) R:
| g1 | g2 | g3 | g4 | g5 | g6 | g7 | g8 | g9 | g10 | g11 | g12 | |
| x1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| x2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| x3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| x4 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| x5 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| x6 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Here, the element Rij is 1 if the top vertex of the X i incident to edge g j and 0 otherwise.
Let’s construct the distance matrix D:
| x1 | x2 | x3 | x4 | x5 | x6 | |
| x1 | 0 | 1 | 1 | 1 | 1 | 1 |
| x2 | 1 | 0 | 1 | 1 | 1 | 2 |
| x3 | 1 | 1 | 0 | 1 | 2 | 2 |
| x4 | 1 | 1 | 1 | 0 | 2 | 2 |
| x5 | 0 | 0 | 0 | 1 | 0 | 1 |
| x6 | 0 | 0 | 0 | 0 | 1 | 0 |
Here, the element Dij is the length the shortest path from vertex X i to vertex X j .
Since our graph is undirected, the distance matrix is symmetric.
We find the distance vector d, each of which is defined as the component
![]() (the maximum distance from the vertex X i to every other vertex).
(the maximum distance from the vertex X i to every other vertex).
Distance vector d = (1, 2, 2, 2, 2, 2). Center is the peak vertex X1 , since it corresponds to the smallest distance (1 = d1 < d j , j = 2,…,6) .
Peripheral tops: X 2 , X 3 , X 4 , X 5 , X 6 , since it corresponds to the maximum remoteness (d j = 2, j = 2,…,6) .
Graph radius G( X ) is the center distance, r(G) = 1 .
Graph diameter G( X ) is the removal of the peripheral vertex, Diam(G) = 2 .
Let’s find the number for the internal and external stability graph. The largest set of internal stability for our graph has the form S = {X 4 , X 5 , X 6 } (the addition of any other peaks will receive adjacent vertices). Accordingly, graph G( X ) number is equal to the internal stability card(T ) = 1.
The smallest set for external stability for our graph is T X1 (as any other vertex (not owned to T) is connected to the apex of X1 from T). The number for the external sustainability graph G( X ) is equal to card(T ) 1.