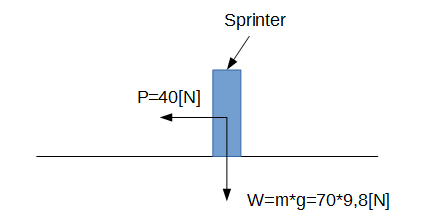Unit: Conversion and Power. Force and Motion
Unit: Conversion and Power
Problem 1. A power station produces 5.609 [GW] of power (1 watt = 1 Joul/1second). How much gasoline should be burned in order to produce the same amount of power? Gasoline has 1,14*
[BTU/gallon] on average.
Solution
BTU is a unit for comparing energy, which stands for British thermal units.
1,14*[BTU/gallon]= 33,41 [kWh/gallon]
1 Joul is equal to 2,78*
[kWh]
Therefore, a power produced in [kWh/s] would be:
P= 5,609*
*2,78*[kWh/s]=1559,3[kWh/s].
The amount of gasoline which should be burned each second in order to produce the same amount of power is:
V=P/33,41=1559,3[kWh/s]/33,41[kWh/gallon]=46,67[gallon/s]
Answer: 46,67 [gallon/s]
Problem 2. The Sun produces 4*
W of power over the whole surface. How many GW power stations on Earth could produce this amount of power?
Solution
From Problem 1 we assume that one power station produces 5.609 [GW] of power.
1 [GW] = 1*[W]
Therefore, 4*[W]=4*
[GW] of power.
The quantity of stations would be: N=4*[GW]/5.609 [GW]=7131396 [units]
Answer: N=7131396 [units]
Unit: Forces and Motion
Problem 3. A sprinter runs the distance of 100 m with a constant acceleration for the first 20 m of the race. The velocity of the sprinter is low enough, so the aerodynamic drag could be neglected. For the first 20 m the sprinter’s legs apply a constant 40 N force parallel to the ground and the sprinter has a mass of 70 kg. Delineate the acceleration of the sprinter due to this force.
Solution
In order to delineate an acceleration, the free body diagram of a sprinter and all external loads which have an impact on the sprinter was drown below.
Second Newton’s law could be applied in this problem case:
ΣF=ma,
where F all forces which are acting on the body, m is mass of the body, and a is an acceleration of the body.
Since in our case an acceleration of the body acts in the horizontal direction. the above equation yields:
P=ma, therefore a=P/m=40[N]/70[kg]=0,57 [
]
Answer: 0,57 []
Problem 4. What is the velocity of the sprinter at the 20 m mark in the preceding problem?
Solution
The velocity at the 20 m mark point could be found from the kinematic equation as follows:
=
+2*a*d, where 
is the velocity at the 20 m point, 
is initial velocity of the sprinter, which in our case equals 0; a is an acceleration, which is constant in this period of the distance and was found in Problem 3 and d is a distance (d=20 m for this problem).
Therefore, =
=
=4,77[m/s]=17,172[km/h]
Answer: 4,77[m/s] or 17,172[km/h]
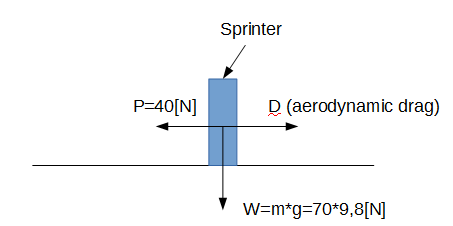
Problem 5. Assume that the sprinter’s legs keep applying a constant force of 60 N parallel to the ground, but for the 50-80 meters section of the track, the velocity is constant. What must be the force of the aerodynamic drag on the sprinter (neglecting other forces)?
Solution
Since the velocity of the sprinter in the section of 50-80 meters is constant and an acceleration is the first derivation of velocity, an acceleration in this section is: a=
=0[]
Therefore, the second Newton’s law in this case would be:
ΣF=0.
In Problem 3, the aerodynamic drag was neglected but for this Problem it is not. Therefore, the free body diagram would be changed, as shown in the picture below.
After substitution of all horizontal forces which act on the sprinter, Newton’s equation will be:
P-D=0, therefore D=P=40[N]
Answer: The aerodynamic drag is 40 [N]
Physics Assistance of Any Level
We hope our solved physics problems were useful and you will manage to accomplish similar assignments yourself. However, if you feel unsure in your technical knowledge and haven’t understood the practical meaning of all the formulas yet, our experts can solve physics problems online for you. We can complete projects of any difficulty level for you and provide you with detailed explanations. Apply for help with physics any time needed.
You are also welcome to look through one of our motion physics examples solved.