Repetition is an algorithmic design that represents a sequence of actions that are performed repeatedly. Algorithms containing a repetition construct are called cyclic, or cycles. The sequence of actions that repeats during the execution of a cycle is called the body of a cycle (or loop). A loop with a given continuation condition is programmed in Pascal using the “while” operator. Sometimes when solving problems, it becomes necessary to perform the body of the loop at least once, and then to investigate the condition to repeat it again. You can go deeper in this question if you check out the following while loop matlab sample.
The while loop example presented here can help you with your own assignment. This sample cannot be presented by you as your own work (unless you will order MATLAB assignment help from us). You can structure your assignment the same as our example. You can also find other samples in our blog that will help you with your tasks. Determine whether you need the following or any other sample, and feel free to use them for your purposes.
MATLAB Practice: For, While loops
The main purpose of the task is to become familiarized with loops in MatLab. A code that solves the following task should contain at least one for and one while loop.
Given:
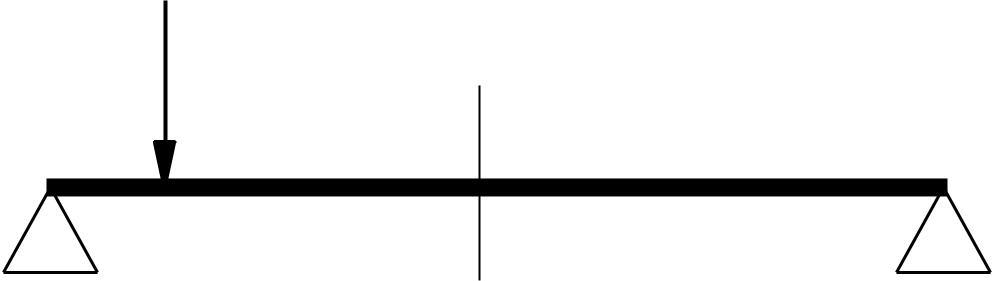
A simply supported beam (see the figure below) with a constant round cross-section. A load moving along the beam.
Find:
The location of the load at which the moment will be maximum and its value.
Find an optimal cross-section parameters (wall thickness, inner and outer radii).
Maximum stress value.
Input parameters that cannot be changed:
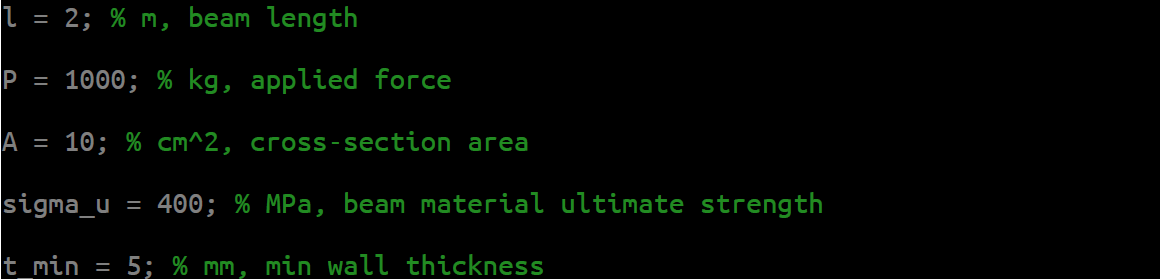
L = 2 m
P = 1,000 kg
σu = 400 MPa
A = 10 cm²
Input limitations:
tmin = 5 mm
Solution
Firstly, we need to declare variables given in the task:
And to convert them to compliant units:
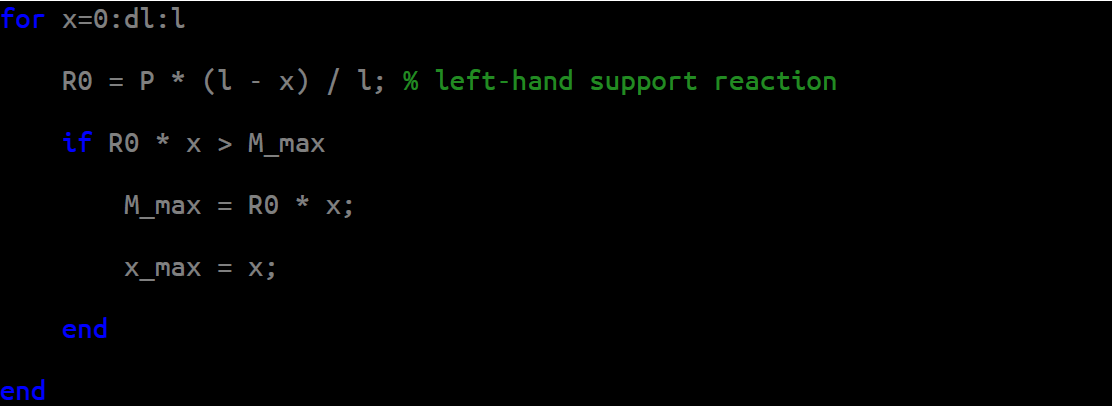
It is obvious that the maximum moment will always be at the load location. So, we will be calculating only those moments. After having chosen the step of the load moving and setting initial values of maximum moment and its location to zero:
We will iterate through the entire length of the beam to find the value of the maximum moment and its location:
It is obvious that it should be at the center of the beam (x = 1 m).
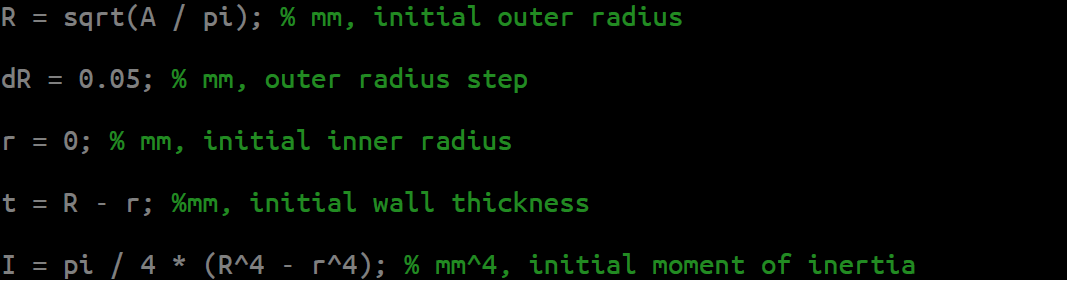
Next, we will assign initial values to cross-section parameter variables.
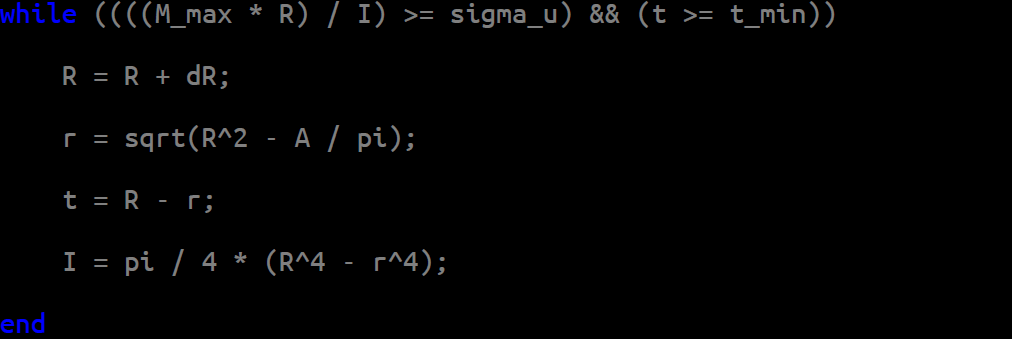
Having initial values, we start increasing the outer radius by the step chosen above until we get such parameters at which acting stresses are less or equal to allowable (σ < σu) and while the wall thickness remains greater or equal to the allowed (t ≥ tmin). Maximum stresses are at the furthest fibers from the neutral axis (σmax = Mmax × R / I):
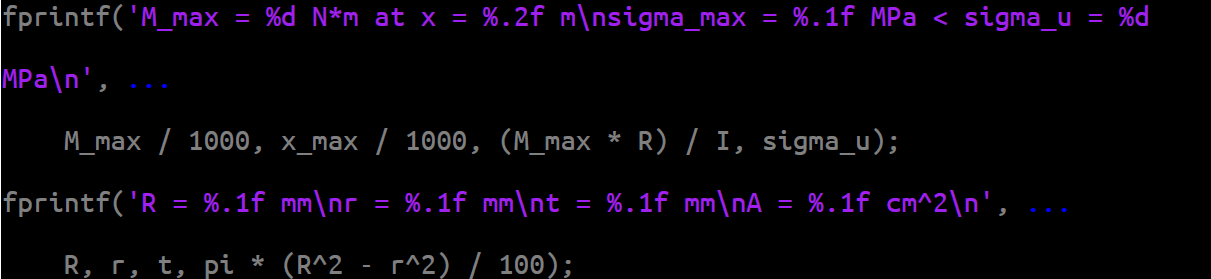
And lastly, we print out the results:
The complete code and the output are shown on the next pages.