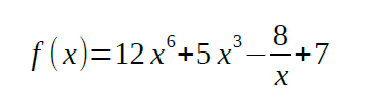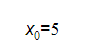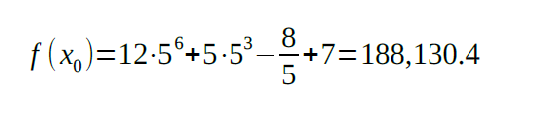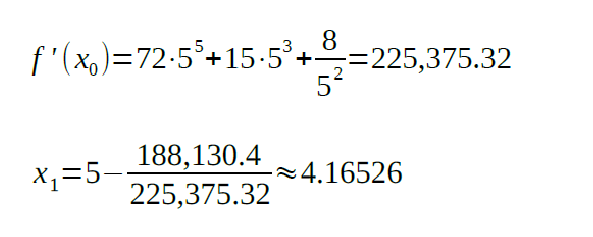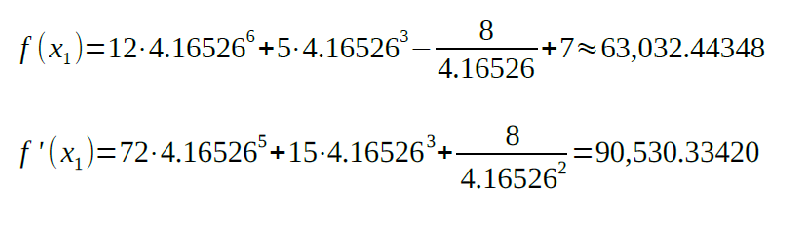Newton Raphson Method Analysis

Find the solution of the following equation using the Newton Raphson Method:

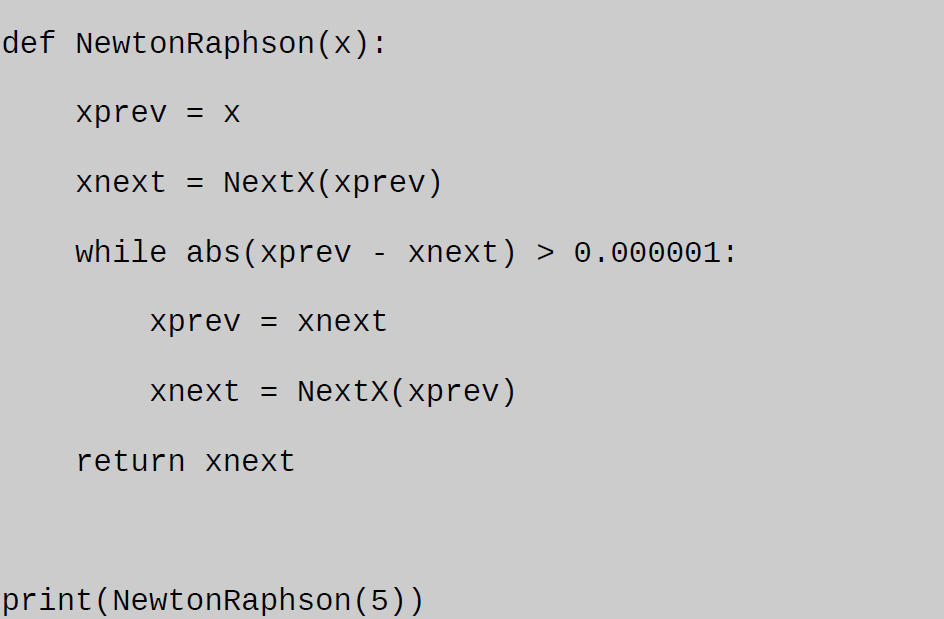
Write a Python 3 code for this method.

Solution

Hand Solution

We must choose an initial value of x:

Let’s plug the above value into the equation:

The next value of x will be found according to the following formula:

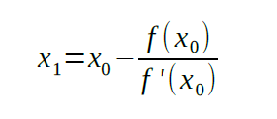
The derivative of the function is:

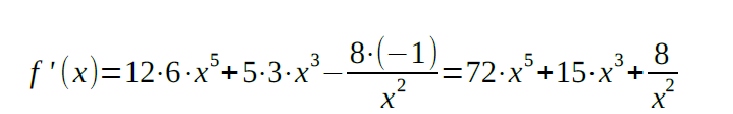
The derivative of the function is:

We will continue finding the next x values until the difference between the adjacent values is small enough:

As the

   

and

   

values are equal, the root of the equation is 0.73518.

Python 3 Code

Firstly, we will define a function for the equation:

Also, we should write a function for numerical calculation of the equation’s derivative. We will use the central difference method with the step of 

   

for each side:

And before writing the main function, we will define a function for the next x value calculation:

Lastly, let’s define the main function:

To simplify reading the variables and find the next x value:

Let’s repeat the above procedure until the difference between the adjacent x values is greater than

   

:

At last, the x value is returned:

The entire code:

Did you find our Newton Raphson method analysis informative and useful? Then you must be craving for other samples of technical assignments developed by our experts. AssignmentShark delivers various articles, samples, and guides on a comprehensive blog you can use to facilitate your academic routine, like you did with this Newton Raphson method example. We specialize in many technical disciplines, namely kinematics, IT, maths, statistics, and engineering. The main goal of our blog is to assist technical major students in their studies.

We have delivered accurate, high-quality academic services for over five years now. AssignmentShark aims to help with assignment writing and run your college errands more effectively and easily and at low prices.