Rotational Motion Examples

Problem 1:
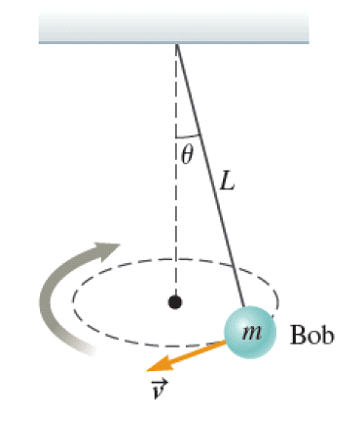
Instead of moving back and forth, a conical pendulum moves in a circle at constant speed as its string traces out a cone (see figure below). One such pendulum is constructed with a string of length L = 0.1m and bob of mass 0.5 kg. The string makes an angle \theta = 5deg with the vertical.

rotation-motion-examples

a. What is the radial acceleration of the bob?
b. What are the horizontal and vertical components of the tension force exerted by the string on the bob? (Assume radially inward to be the positive x axis and vertically upward to be the positive y axis. Express your answer in vector form.)

Solution:

a.

a_r = \frac{v^2}{r}

Tcos\theta = mg \Rightarrow T = \frac{mg}{cos\theta}

Tsin\theta = m\frac{v^2}{r}

\Rightarrow \frac{v^2}{r} = \frac{Tsin\theta}{m} = \frac{mgsin\theta}{mcos\theta} = gtan\theta

a_r = \frac{v^2}{r} = gtan\theta = 9.81*0.087 = 0.86 m/s^2

b.

T_y = Tcos\theta = mg = 0.5*9.81 = 4.9N

T_x = Tsin\theta = m\frac{v^2}{r} = 0.5 * 0.86 = 0.43N

T = T_x \vec{i} + T_y\vec{j} = 0.43\vec{i} + 4.9\vec{j}N

Answer: a_r = 0.86 m/s^2 and T = 0.43\vec{i} + 4.9\vec{j}N

Problem 2:

A block of mass M is placed on a frictionless plane. The plane is inclined at an angle \theta, and the block is a distance d from its end. Of course, we would expect the block to slip down the plane. Suppose we revolve the incline around the vertical axis shown in the figure below instead. At what period of revolution will the block remain in place on the plane?

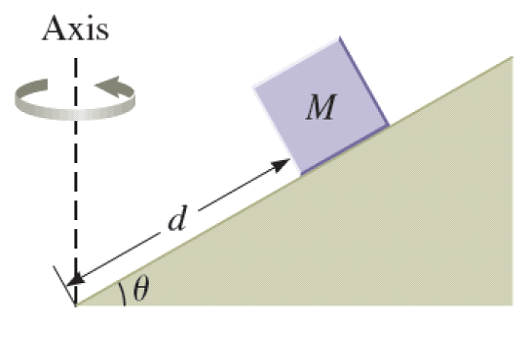
rotation-motion-example-2

Solution:

The block will be remain at the same location if all forces influencing on it are in equilibrium.

Therefore, the centrifugal force:

m\omega^2 r = N sin \theta

Where N is a reaction of the block

m\omega^2 r = \frac{mg}{cos\theta}sin\theta

\omega = \sqrt{\frac{gtan\theta}{d}}

T = \frac{2\pi}{\omega} = 2\pt\sqrt{\frac{d}{gtan\theta}}

Answer: T = 2\pi \sqrt{\frac{d}{gtan\theta}}

Math Homework Assistance from the Experts

What do you think about our rotational motion examples? Do you find them useful? We hope that our examples will help you with solving your tasks and you didn’t miss the previous one about the law of conservation of energy problems with solutions. If not you can always apply to AssignmentShark for help with assignments.

Our service was established for students that need to get help with technical tasks. If you can’t solve your assignment in math, physics, or programming you can’t plagiarize any work from the Web. The only way out is to get “do my math homework for money” assistance from knowledgeable person. We offer you the ability to get help from well-qualified experts. You should only specify the requirements on our website and keep in touch with the expert during the whole process. Look through our rotational motion examples one more time and make your final decision! We are waiting for you 24/7!

Leave a Reply

Your email address will not be published. Required fields are marked *

Customer testimonials

    Submit your instructions to the experts without charge.