Problem 1:
An intrepid physics student decides to try bungee jumping. She obtains a cord that is ![]() m long and has a spring constant of
m long and has a spring constant of ![]() . When fully suited, she has a mass of
. When fully suited, she has a mass of ![]() . She looks for a bridge to which she can tie the cord and step off. Determine the minimum height of the bridge L, that will allow her to stay dry (that is, so that she stops just before hitting the water below). Assume air resistance that is negligible.
. She looks for a bridge to which she can tie the cord and step off. Determine the minimum height of the bridge L, that will allow her to stay dry (that is, so that she stops just before hitting the water below). Assume air resistance that is negligible.
Solution:
From the conservation of energy, we have kinetic and elastic energies that have transformed into potential energy:
![]()
Where
![]()
Therefore
![]()
![]()
![]()
![]()
![]()
We have two solutions:
![]() and
and ![]()
The height of the bridge can’t be less than length of cord, therefore we select only ![]() m.
m.
Answer: ![]() m.
m.
Problem 2:
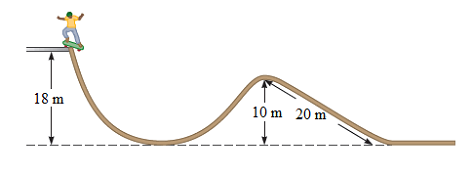
Tony Hawk ![]() rides his skateboard at a local skate park. He starts from rest at the top of the track as seen in the figure below and begins a descent down the track, always maintaining contact with the surface. The mass of the skateboard is negligible, as is friction except where noted.
rides his skateboard at a local skate park. He starts from rest at the top of the track as seen in the figure below and begins a descent down the track, always maintaining contact with the surface. The mass of the skateboard is negligible, as is friction except where noted.
(a) What is Shawn’s speed when he reaches the bottom of the initial dip, 18.0 m below the starting point?
(b) He then ascends the other side of the dip to the top of a hill, 8.0 m above the ground. What is his speed when he reaches this point?
Solution:
a. From the conservation of energy: Potential energy at the top of the 18 m transforms into the Kinetic energy at the bottom of the dip.
![]()
![]()
b. From the conservation of energy: Potential energy at the top of the 18 m transforms into the Kinetic and Potential energy at the top of a hill.
![]()
![]()
![]()
Answer ![]() and
and ![]()
Solutions of Your Physics Homework Problems
While you are reading our sample on the law of conversation of energy problems, you can get some ideas on how to deal with your own assignment. Always look through our samples before starting doing your homework, as they can help you to deal with it successfully. Remember that there is a service that can provide you with online physics homework help – AssignmentShark.com. Request solve my physics problem help, provide us with your requirements and set the deadline while you are placing an order. Our experts can deal with any assignment of any difficulty level. You can discuss your order with an expert directly via chat. Explore new opportunities to deal with your assignment successfully with our service!
You can also like one of our rotational motion examples.